2025-12-10 08:01:12
⚡️ Співвідношення між кутами і сторонами в прямокутному трикутнику
Тригонометричні функції — це один із найпотужніших інструментів для роботи з прямокутними трикутниками. У попередніх матеріалах ми вже розібрали їх означення та основні випадки (30°, 45°, 60°). Тепер — завершуємо тему й підсумовуємо універсальні формули, які дозволяють розв’язати будь-який прямокутний трикутник, якщо відомий один гострий кут і будь-яка сторона.
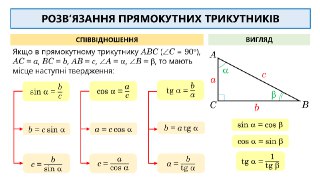
🔍 Прямокутний трикутник із кутами α і β.
Нехай катети: 𝐴𝐶 = 𝑎, 𝐵𝐶 = 𝑏; гіпотенуза: 𝐴𝐵 = 𝑐.
Кути: ∠𝐴 = 𝛼, ∠𝐵 = 𝛽 (див. скриншот).
✈️ Формули через синус
Катет = гіпотенуза ⋅ синус протилежного кута
🔍 якщо sin 𝛼 = 𝑏/𝑐, то 𝑏 = 𝑐 sin 𝛼
🔍 якщо sin 𝛽 = 𝑎/𝑐, то 𝑎 = 𝑐 sin 𝛽
Гіпотенуза = катет / синус протилежного кута
🔍 якщо sin 𝛼 = 𝑏/𝑐, то 𝑐 = 𝑏/sin 𝛼
🔍 якщо sin 𝛽 = 𝑎/𝑐, то 𝑐 = 𝑎/sin 𝛽
✈️ Формули через косинус
Катет = гіпотенуза ⋅ косинус прилеглого кута
🔍 якщо cos 𝛼 = 𝑎/𝑐, то 𝑎 = 𝑐 cos 𝛼
🔍 якщо cos 𝛽 = 𝑏/𝑐, то 𝑏 = 𝑐 cos 𝛽
Гіпотенуза = катет / косинус прилеглого кута
🔍 якщо cos 𝛼 = 𝑎/𝑐, то 𝑐 = 𝑎/cos 𝛼
🔍 якщо cos 𝛽 = 𝑏/𝑐, то 𝑐 = 𝑏/cos 𝛽
✈️ Формули через тангенс
Катет = інший катет ⋅ тангенс протилежного кута
🔍 якщо tg 𝛼 = 𝑏/𝑎, то 𝑏 = 𝑎 tg 𝛼
🔍 якщо tg 𝛽 = 𝑎/𝑏, то 𝑎 = 𝑏 tg 𝛽
Катет = інший катет / тангенс прилеглого кута
🔍 якщо tg 𝛼 = 𝑏/𝑎, то 𝑎 = 𝑏/tg 𝛼
🔍 якщо tg 𝛽 = 𝑎/𝑏, то 𝑏 = 𝑎/tg 𝛽
❗️ Важливо! Не обов'язково завчати всі ці формули. Набагато корисніше тренувати уміння будувати потрібну пропорцію:
1️⃣ Запишіть тригонометричну функцію відомого кута (sin, cos або tg).
2️⃣ Оберіть ту, що містить і відомий відрізок, і той, який треба знайти.
3️⃣ Звичайною пропорцією виразіть невідому величину.
Це універсальний алгоритм, який працює завжди.
📸 Приклади розв'язання завдань дивіться на скриншотах.
💬 Задавайте свої питання в коментарях!
🇺🇦@abitmath 🇺🇦@abitblog
Тригонометричні функції — це один із найпотужніших інструментів для роботи з прямокутними трикутниками. У попередніх матеріалах ми вже розібрали їх означення та основні випадки (30°, 45°, 60°). Тепер — завершуємо тему й підсумовуємо універсальні формули, які дозволяють розв’язати будь-який прямокутний трикутник, якщо відомий один гострий кут і будь-яка сторона.
🔍 Прямокутний трикутник із кутами α і β.
Нехай катети: 𝐴𝐶 = 𝑎, 𝐵𝐶 = 𝑏; гіпотенуза: 𝐴𝐵 = 𝑐.
Кути: ∠𝐴 = 𝛼, ∠𝐵 = 𝛽 (див. скриншот).
✈️ Формули через синус
Катет = гіпотенуза ⋅ синус протилежного кута
🔍 якщо sin 𝛼 = 𝑏/𝑐, то 𝑏 = 𝑐 sin 𝛼
🔍 якщо sin 𝛽 = 𝑎/𝑐, то 𝑎 = 𝑐 sin 𝛽
Гіпотенуза = катет / синус протилежного кута
🔍 якщо sin 𝛼 = 𝑏/𝑐, то 𝑐 = 𝑏/sin 𝛼
🔍 якщо sin 𝛽 = 𝑎/𝑐, то 𝑐 = 𝑎/sin 𝛽
✈️ Формули через косинус
Катет = гіпотенуза ⋅ косинус прилеглого кута
🔍 якщо cos 𝛼 = 𝑎/𝑐, то 𝑎 = 𝑐 cos 𝛼
🔍 якщо cos 𝛽 = 𝑏/𝑐, то 𝑏 = 𝑐 cos 𝛽
Гіпотенуза = катет / косинус прилеглого кута
🔍 якщо cos 𝛼 = 𝑎/𝑐, то 𝑐 = 𝑎/cos 𝛼
🔍 якщо cos 𝛽 = 𝑏/𝑐, то 𝑐 = 𝑏/cos 𝛽
✈️ Формули через тангенс
Катет = інший катет ⋅ тангенс протилежного кута
🔍 якщо tg 𝛼 = 𝑏/𝑎, то 𝑏 = 𝑎 tg 𝛼
🔍 якщо tg 𝛽 = 𝑎/𝑏, то 𝑎 = 𝑏 tg 𝛽
Катет = інший катет / тангенс прилеглого кута
🔍 якщо tg 𝛼 = 𝑏/𝑎, то 𝑎 = 𝑏/tg 𝛼
🔍 якщо tg 𝛽 = 𝑎/𝑏, то 𝑏 = 𝑎/tg 𝛽
❗️ Важливо! Не обов'язково завчати всі ці формули. Набагато корисніше тренувати уміння будувати потрібну пропорцію:
1️⃣ Запишіть тригонометричну функцію відомого кута (sin, cos або tg).
2️⃣ Оберіть ту, що містить і відомий відрізок, і той, який треба знайти.
3️⃣ Звичайною пропорцією виразіть невідому величину.
Це універсальний алгоритм, який працює завжди.
📸 Приклади розв'язання завдань дивіться на скриншотах.
💬 Задавайте свої питання в коментарях!
🇺🇦@abitmath 🇺🇦@abitblog