2025-09-03 12:01:08
✨ Раціональні, ірраціональні та дійсні числа
Ми вже познайомилися з натуральними та цілими числами, а тепер настав час розглянути останні важливі множини, без яких неможливо уявити сучасну математику.
🔍 Раціональні числа — це числа, які можна записати у вигляді дробу 𝑚/𝑛, де 𝑚 — ціле число, а 𝑛 — натуральне число.
✈️ Позначення: 𝑄.
✈️ Приклади: –7/9; 2,75; –0,(3) — усі вони є раціональними.
✈️ Зверніть увагу: навіть «звичайні» числа, як-от 8, –3 чи 0, також належать до раціональних, бо їх можна записати як 8/1, –3/1, 0/1.
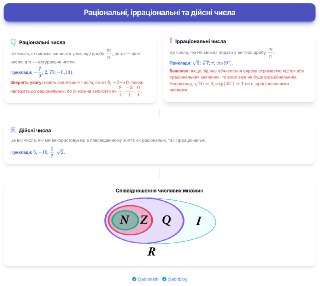
Отже, усі цілі числа входять до множини раціональних чисел. У свою чергу, усі натуральні числа входять у склад цілих (див. Цілі числа та їх особливості).
✈️ Ірраціональні числа — це числа, які НЕ можна подати у вигляді дробу 𝑚/𝑛.
✈️ Позначення: 𝐼.
✈️ Приклади: √3; ∛7; 𝜋; cos(9°) — це ірраціональні числа.
✈️ Важливо: якщо під час обчислення виразу отримаємо «ціле» або «дробове» значення, то воно вже не буде ірраціональним. Наприклад, √16 = 4 і tg(45°) = 1 не є ірраціональними числами.
✈️ Дійсні числа — це всі числа, які ми використовуємо у шкільній математиці: як раціональні, так і ірраціональні.
✈️ Позначення: 𝑅.
🌍 Фактично, множина дійсних чисел охоплює всі відомі нам числові величини — від ціни товару чи температури повітря до нескінченного числа 𝜋.
🇺🇦@abitmath 🇺🇦@abitblog
Ми вже познайомилися з натуральними та цілими числами, а тепер настав час розглянути останні важливі множини, без яких неможливо уявити сучасну математику.
🔍 Раціональні числа — це числа, які можна записати у вигляді дробу 𝑚/𝑛, де 𝑚 — ціле число, а 𝑛 — натуральне число.
✈️ Позначення: 𝑄.
✈️ Приклади: –7/9; 2,75; –0,(3) — усі вони є раціональними.
✈️ Зверніть увагу: навіть «звичайні» числа, як-от 8, –3 чи 0, також належать до раціональних, бо їх можна записати як 8/1, –3/1, 0/1.
Отже, усі цілі числа входять до множини раціональних чисел. У свою чергу, усі натуральні числа входять у склад цілих (див. Цілі числа та їх особливості).
✈️ Ірраціональні числа — це числа, які НЕ можна подати у вигляді дробу 𝑚/𝑛.
✈️ Позначення: 𝐼.
✈️ Приклади: √3; ∛7; 𝜋; cos(9°) — це ірраціональні числа.
✈️ Важливо: якщо під час обчислення виразу отримаємо «ціле» або «дробове» значення, то воно вже не буде ірраціональним. Наприклад, √16 = 4 і tg(45°) = 1 не є ірраціональними числами.
✈️ Дійсні числа — це всі числа, які ми використовуємо у шкільній математиці: як раціональні, так і ірраціональні.
✈️ Позначення: 𝑅.
🌍 Фактично, множина дійсних чисел охоплює всі відомі нам числові величини — від ціни товару чи температури повітря до нескінченного числа 𝜋.
🇺🇦@abitmath 🇺🇦@abitblog